2.2最大鋪展因子βmax

2.2.1毛細(xì)力主導(dǎo)區(qū)

如表1所示，不同學(xué)者給出的毛細(xì)力區(qū)（P<1）βmax模型存在差異，但都認(rèn)為與We密切相關(guān)，而與Re無關(guān)。Fedorchenko等通過理論推導(dǎo)、Eggers等利用數(shù)值模擬，認(rèn)為βmax∝We0.5,但Eggers是在假設(shè)壁面完全疏水（θe=180°）的前提下得出該結(jié)論。Bartolo等、Antonini等、Clanet等通過實驗研究，得出βmax∝We0.25;Clanet等和Bartolo等認(rèn)為無論壁面潤濕性如何，該規(guī)律均適用，但Antonini等則認(rèn)為當(dāng)We<200時，壁面疏水性會導(dǎo)致βmax偏離該規(guī)律。

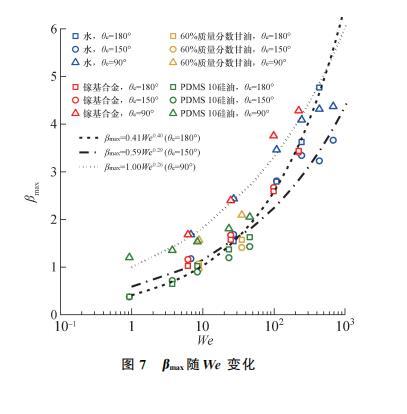
本文在毛細(xì)力區(qū)研究的流體包括水、60%質(zhì)量分?jǐn)?shù)甘油溶液、PDMS10硅油和鎵基合金，βmax隨We變化的情況如圖7所示。對不同潤濕性壁面的模擬結(jié)果進(jìn)行擬合，如圖7中虛線所示：當(dāng)θe=90°時，βmax∝We0.26（R2=0.921）；當(dāng)θe=180°時，βmax∝We0.40（R2=0.990）；當(dāng)θe=150°時，βmax∝We0.29（R2=0.918），介于前兩者之間。因為真實表面無法絕對疏水，所以Clanet等實驗研究結(jié)果βmax∝We0.25更接近本文θe=90°的模擬結(jié)果，而Eggers等針對完全疏水表面提出的βmax∝We0.5更適用于θe=180°的情況。

雖然圖7中的4種流體物性差異較大，但模擬結(jié)果整體分布在以We為變量的冪函數(shù)曲線附近，說明在毛細(xì)力區(qū)，We是βmax的主要控制因素。從圖7中3條擬合曲線的指數(shù)變化可以看出，隨著壁面疏水性增強(qiáng)，黏性力對液滴鋪展的阻礙作用減弱，液滴的βmax隨之增大，導(dǎo)致θe=180°時βmax∝Web規(guī)律的指數(shù)b最大。

2.2.2黏性力主導(dǎo)區(qū)

如表1所示，文指出在黏性力主導(dǎo)區(qū)（P>1）存在規(guī)律βmax∝Re0.2.本文在黏性力區(qū)的研究采用3種質(zhì)量分?jǐn)?shù)的甘油溶液、3種型號的PDMS甘油，黏度變化范圍為10——970 mPa·s,跨越近3個數(shù)量級。其中，黏度極高的PDMS1000硅油在低速碰撞壁面時有Re=1.

βmax隨Re變化情況如圖8所示，圖中虛線為碰撞不同潤濕性壁面的擬合結(jié)果：當(dāng)θe=90°時，βmax∝0.93Re0.19（R2=0.980）；當(dāng)θe=150°時，βmax∝Re0.27（R2=0.953）。可以看出，θe=90°的數(shù)據(jù)整體落在了θe=150°數(shù)據(jù)的上方，但隨著Re增大，二者的差異逐漸減小。由此可見在黏性力區(qū)，液滴碰撞親水壁面的βmax更大；但隨著Re增加，黏性力影響減弱，與黏性力相關(guān)聯(lián)的壁面潤濕性影響隨之減弱，此時疏水壁面上βmax迅速增加，導(dǎo)致βmax∝Reb規(guī)律的指數(shù)b更大。

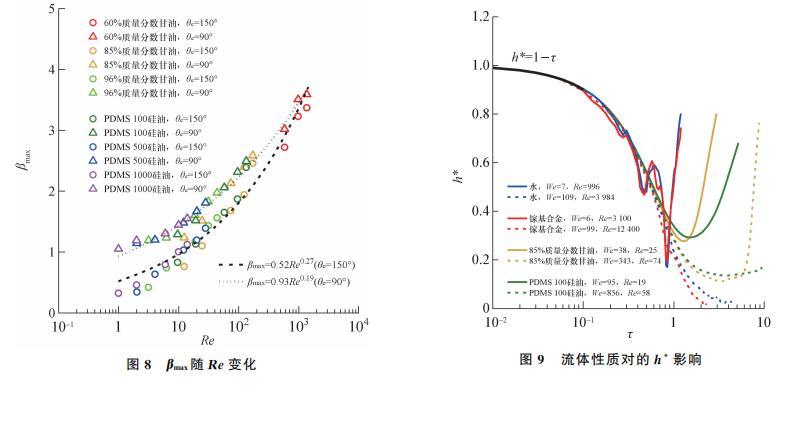
圖8βmax隨Re變化

當(dāng)Re趨近于1時，數(shù)據(jù)點明顯偏離擬合曲線，這是因為高黏度液滴低速度碰撞壁面時，入射動能很快通過黏性力耗散殆盡，液滴鋪展基本不受慣性力影響，近似于自然鋪展，導(dǎo)致βmax與Re關(guān)聯(lián)性減弱。

2.3液滴中心厚度h*隨時間變化

圖9給出了表2中4種流體在θe為150°的壁面上的h——τ曲線。當(dāng)τ<0.1時，無論We、Re如何變化，均有規(guī)律h=1-τ,說明該階段h受慣性力主導(dǎo)。當(dāng)We較大時，液滴的高入射速度和低表面張力使h出現(xiàn)平臺期。對于水和鎵基合金，當(dāng)We<10時，h*隨時間變化具有明顯波動性，這說明在低速入射的情況下，高表面張力會導(dǎo)致液滴厚度產(chǎn)生振蕩，這與Wang等在水滴碰撞實驗中觀測到的現(xiàn)象一致。

如表1所示，文認(rèn)為hmin僅與Re相關(guān)。從圖9中甘油溶液和PDMS硅油的曲線可以看出，二者Re相近，hmin幾乎相同，與已有結(jié)論一致；但對于We相近、Re相差較大的水和鎵基合金，二者也有相似的hmin.因此，hmin是否僅與Re相關(guān)，需要進(jìn)一步探討。

2.4最小中心厚度hmin*

如表所示，Roisman等和Fedorchenko等通過理論推導(dǎo)，Eggers等通過數(shù)值模擬，發(fā)現(xiàn)當(dāng)Re較大時有hmin∝Re-0.4,Lagubeau等通過實驗測量支持了該結(jié)論。當(dāng)Re<1000時，Du等和Eggers等通過模擬研究，認(rèn)為此時可以忽略雙曲流影響，有hmin∝Re-0.5.也有研究認(rèn)為當(dāng)We較小時，表面張力顯著影響液滴厚度。

由于h達(dá)到hmin時，液滴的中心比邊緣要薄，因此很難通過拍攝手段獲得準(zhǔn)確數(shù)據(jù)，并且已有結(jié)論主要基于水和甘油溶液，體系覆蓋范圍有限。因此，本文對表2中9組流體進(jìn)行碰撞模擬，得到hmin*隨Re變化的情況如圖10所示（水和鎵基合金低速碰撞θe為90°的壁面時，液滴中心劇烈振蕩無穩(wěn)定模擬結(jié)果，故剔除這部分?jǐn)?shù)據(jù)）。

本文所研究的碰撞體系大部分滿足Re<1000,因此與文中規(guī)律hmin∝Re-0.5比較。對We≥10、Re<1000的數(shù)據(jù)擬合得到hmin=1.20Re-0.50（R2=0.955）。可以看出空心數(shù)據(jù)點大多落在該擬合曲線上，本文模擬結(jié)果與文的結(jié)論一致。從2種形狀的空心數(shù)據(jù)點在擬合曲線上基本重合可以看出，壁面潤濕性對We≥10液滴的hmin*——Re關(guān)系無顯著影響。

We<10的實心數(shù)據(jù)點整體分布在擬合曲線上方，且不同θe對應(yīng)的hmin相差較大。當(dāng)We=1時，液滴碰撞θe為150°的壁面的hmin比擬合曲線hmin=1.20Re-0.50高出197.53%.這一現(xiàn)象證實了Zhu等的研究結(jié)論：We較小時，表面張力和壁面潤濕性對hmin產(chǎn)生明顯影響。因此本文認(rèn)為，hmin*主要受Re控制的理論僅適用于We較大的情況。

此外，當(dāng)Re接近于1時，hmin明顯偏離hmin∝Re-0.5規(guī)律，其原因與上文所述一致，即高黏度液滴低速碰撞壁面時，液滴更多的表現(xiàn)出自然鋪展特性。

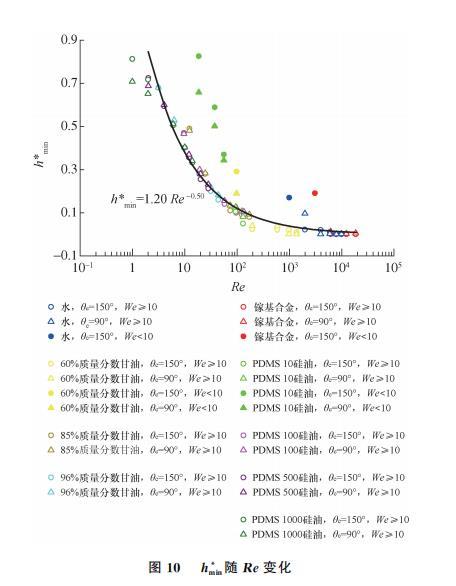
圖10 hmin*隨Re變化

3結(jié)論

本文利用相場法，數(shù)值模擬了9組流體碰撞不同潤濕性壁面的過程，拓展了液滴碰撞模擬研究的流體物性范圍，主要結(jié)論如下：

1）在碰撞初期（τ<0.1），發(fā)現(xiàn)文提出的規(guī)律β∝τ0.5主要適用于Re>100的液滴碰撞，這是因為低Re液滴的黏性力較強(qiáng)，慣性力不再處于主導(dǎo)地位；h的模擬結(jié)果符合已有結(jié)論h=1-τ,說明在碰撞初期，h*主要受慣性力影響。

2）在毛細(xì)力區(qū)，本文模擬結(jié)果顯示βmax∝Web,符合前人研究結(jié)論；隨著壁面疏水性增強(qiáng)，指數(shù)b逐漸增大，說明當(dāng)毛細(xì)力主導(dǎo)鋪展時，壁面越疏水，黏性力對鋪展的阻礙作用越小，βmax越大。在黏性力區(qū)，數(shù)值結(jié)果滿足規(guī)律βmax∝Reb,與已有理論相符；當(dāng)液滴Re較小時，親水壁面上的βmax更大，但隨著Re增大，慣性力增強(qiáng)，壁面潤濕性的影響隨之減弱，疏水壁面上的βmax迅速增加，導(dǎo)致βmax∝Reb規(guī)律的指數(shù)b較大。

3）當(dāng)We≥10、Re<1000時，hmin模擬結(jié)果與文提出的規(guī)律hmin∝Re-0.5相符，但We<10時會偏離該規(guī)律，壁面潤濕性和表面張力對hmin產(chǎn)生明顯影響。其機(jī)理在于低We液滴的毛細(xì)力較強(qiáng)，高表面張力和壁面疏水性減弱了液滴的鋪展能力，所以不能再僅依據(jù)Re去預(yù)測hmin.

4）對于以往鮮有研究的高黏度PDMS1000硅油和超高表面張力的鎵基合金，盡管這2種流體物性較為特殊，但其碰撞過程仍主要受Re和We影響。但當(dāng)PDMS1000硅油以低速碰撞壁面時，Re接近于1,此時液滴的入射動能很快通過黏性力耗散殆盡，慣性力作用可忽略不計，液滴在壁面上近似于自發(fā)鋪展，導(dǎo)致βmax和hmin*主要由液滴初始動能和壁面潤濕性決定，偏離結(jié)論2和3中與We、Re之間的冪函數(shù)關(guān)系。